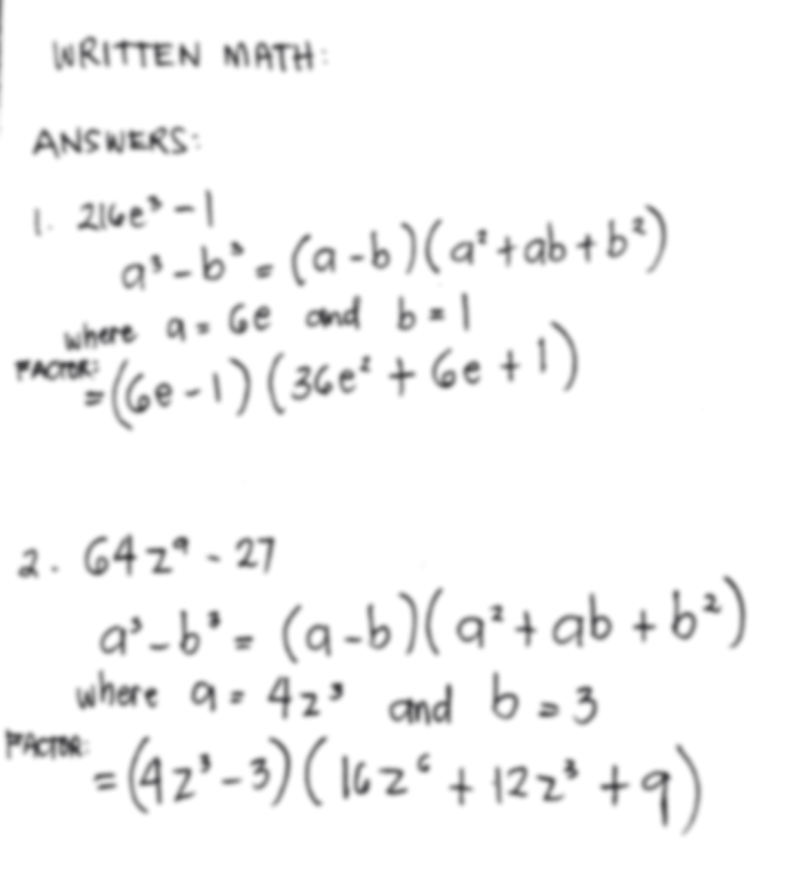Factoring The Sum Or Difference Of Cubes – Something or something or something. Where something is a factor of 3. Example: 2 2 2 = 8, so 8 is a perfect cube. x2 x2 x2 = x6 so x6 is a perfect cube. It is easy to see that a variable is a perfect cube. See if the exponent is divisible by 3.
There are two terms The terms are separated by a + or – sign Each term is a perfect cube. The sum or difference of two cubes will convert into a trinomial binomial .
Factoring The Sum Or Difference Of Cubes

Now that we know how to get the signals, let’s work on what is going on inside. Square this term to get this term. Cube Root of the First Term Product of the cube root of the first term and the cube root of the second term. Cube root of the second term
Factoring Sum Or Difference Of Two Cubes Worksheet
Factor this difference in cubes. Watch out for your signs!!! Cube Root 3x 5 9×2 15x 25 of the first term Multiply them to get this. Square this term to get this term. Cube root of the second term Square this term to get this term. You did it! I hope you took notes because I’m done here!!!
Example 2: Factor each of the following polynomials 8×3 – 27 = (2x – 3)((2x)2 + (2x)(3) + (3)2) Use the pattern a3 – b3 = (a – b)( a2 + ab + b2) = (2x – 3)(4×2 + 6x + 9) b) 9×4 – 9x = 9x(x3 – 1) First eliminate GCF = 9x(x – 1)(x2 + x + 1) Difference of the factor of the cubes x3 – 1
In order for this site to function, we record and share user data with processors. To use this website, you must agree to our Privacy Policy, including our cookie policy.
Sum/difference of cubes factors: a3 + b3 = (a + b)(a2 – ab + b2) a3 – b3 = (a – b)(a2 + ab + b2) Sum of cubes Difference of cubes
Solved:sum Or Difference Of Cubes Factor The Sum Or Difference Of…
Example 1: Complete each of the following polynomials. s3 + t3 = (s + t)(s2 – st + t2) v3 – w3 = (v – w)(v2 + vw + w2)
Example 2: Complete each of the following polynomials. 8×3 – 27 = (2x – 3)((2x)2 + (2x)(3) + (3)2) Use the pattern a3 – b3 = (a – b)(a2 + ab + b2) = (2x – 3)(4×2 + 6x + 9) b) 9×4 – 9x = 9x(x3 – 1) Solve GCF = 9x(x – 1)(x2 + x + 1) first Differentiate the cubes of x3 – 1 a take into account
6 Homework Do #1 – 19 odd questions only on page 120 section 4.2 for Thursday

In order for this site to work, we record and share user data with processors. To use this website, you must agree to our Privacy Policy, including our cookie policy. In algebra class, the teacher always discussed the subject of the sum of two cubes and the difference between two side by side cubes. The reason is that they are similar in structure. The key is to “remember” or remember the patterns associated with the formulas.
Factoring Sum/difference Of Cubes
So here are the formulas that summarize how to factor the sum and difference of two cubes. Study them carefully.
Rewrite the original problem as two cubes and then simplify. Since this is the “sum” case, the binomial factor and the trinomial factor will have positive and negative mean signs, respectively.
Apply the rule for the difference of two cubes and simplify. Since this is the case of the “difference”, the binomial factor and the trinomial factor will have negative and positive average signs, respectively.
At first, this problem may seem “hard”. However, if we stick to what we already know about the sum and difference of two cubes, we should be able to recognize that this problem is relatively easy.
Factoring Sum And Difference Of Two Cubes
Sometimes the problem seems to ignore the sum or difference of the two cubes. If you see something like this, try to eliminate the common factors. For numbers, the greatest common factor is [latex]3[/latex], and for variables, the greatest common factor is “[latex]xy[/latex]”. Therefore, the general common factor of their product is [latex] left(3 right) left( right) = 3xy[/latex].
After factoring, you will see that we have an easy problem with the difference between two cubes.
Factoring sum and difference of cubes worksheet, factoring the sum or difference of cubes worksheet answers, factoring the sum of two cubes, factoring sum and difference of cubes calculator, factoring the sum or difference of cubes worksheet, factoring sum or difference of two cubes, factoring polynomials sum and difference of cubes, factoring the sum or difference of cubes calculator, factoring sum difference of cubes, sum or difference of two cubes, sum or difference of cubes, factoring a sum or difference of cubes